-
Hanota Problem
def hanota(A: list[int], B:List[int], C:List[int]): n=len(A) if n==1: C.append(A.pop()) else: hanota(A, C, B) C.append(A.pop()) hanota(B, A, C)A,B,C表示三个柱子,初始状态为A中有降序的数字,代表大小的盘子。
思路:递归问题,当盘子数量大于1时,归纳为三个步骤:
-
把n-1个盘子从A移到B
-
把最后一个盘子从A移到C
-
把B上的盘子移到C
-
-
用切片实现去除字符串首尾空格:
def trim(s): if s[:1] == ' ': return trim(s[1:]) if s[-1:] == ' ': return trim(s[:-1]) return s -
两数之和
问题描述:给定一个整数数组
nums和一个整数目标值target,请你在该数组中找出 和为目标值target的那 两个 整数,并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9 输出:[0,1] 解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6 输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6 输出:[0,1]
提示:
2 <= nums.length <= 104-109 <= nums[i] <= 109-109 <= target <= 109- 只会存在一个有效答案
进阶:你可以想出一个时间复杂度小于
O(n²)的算法吗?解题思路:
问题核心是:数组中是否存在目标数字-当前数字的数,存在,则返回两个数的下标。
依次遍历数组中的数字,并计算差,若差数未遍历到,则先存放,若已遍历到,则返回下标。
DEMO:
class Solution: def twoSum(nums:List[int], target:int)->List[int]: num_list={} for i, num in enumerate(nums): complement=target-num if complement in num_list: return [num_list[complement], i] else: num_list[num]=i -
两数相加
问题描述:
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:
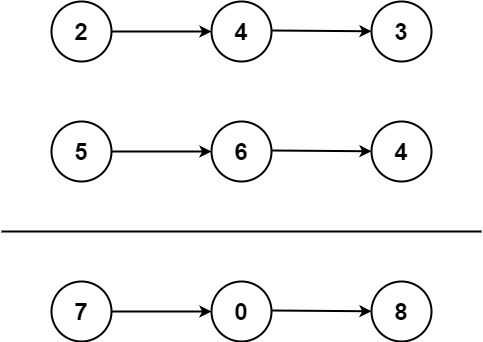
输入:l1 = [2,4,3], l2 = [5,6,4] 输出:[7,0,8] 解释:342 + 465 = 807.示例 2:
输入:l1 = [0], l2 = [0] 输出:[0]示例 3:
输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9] 输出:[8,9,9,9,0,0,0,1]提示:
- 每个链表中的节点数在范围
[1, 100]内 0 <= Node.val <= 9- 题目数据保证列表表示的数字不含前导零
解题思路:
为了实现两个链表的逆序相加,可以按照以下步骤进行:
- 从头到尾遍历两个链表,逐位相加。
- 将每一位的和与上一位的进位相加,得到新的进位。
- 创建一个新的链表,将每一位的和的个位数添加到新链表,并更新进位。
- 如果两个链表的长度不同,处理剩余的部分。
DEMO:
class ListNode: def _init_(self,val=0,next=None): self.val=val self.next=next def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]: dummy=ListNode() current=dummy carry=0 while l1 or l2 or carry: x=l1.val if l1 else 0 y=l2.val if l2 else 0 sumn=x+y+carry carry=sumn//10 current.next=ListNode(sumn%10) current=current.next if l1: l1=l1.next if l2: l2=l2.next return dummy.next dummy = ListNode() # 创建一个虚拟头结点 current = dummy # 用于迭代的指针 carry = 0 # 进位 while l1 or l2 or carry: # 获取 l1 和 l2 当前节点的值,如果为空则为0 x = l1.val if l1 else 0#三元表达式,如果 l1 存在(不为 None),则将 x 赋值为 l1.val,否则将 x 赋值为 0。 y = l2.val if l2 else 0 # 计算当前位的和,加上上一位的进位 _sum = x + y + carry # 计算新的进位 carry = _sum // 10 # 创建新的节点,将个位数添加到新链表 current.next = ListNode(_sum % 10) current = current.next # 移动 l1 和 l2 指针 if l1: l1 = l1.next if l2: l2 = l2.next return dummy.next # 返回虚拟头结点的下一个节点,即新链表的头结点,以返回整个链表 - 每个链表中的节点数在范围
-
无重复字符的最小子串。
给定一个字符串
s,请你找出其中不含有重复字符的 最长子串 的长度。示例 1:
输入: s = "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。示例 2:
输入: s = "bbbbb" 输出: 1 解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。示例 3:
输入: s = "pwwkew" 输出: 3 解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。 请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。提示:
0 <= s.length <= 5 * 104s由英文字母、数字、符号和空格组成
解题思路:通过遍历字符串中的字符,动态地调整滑动窗口的位置。
char_index_map字典用于存储字符及其最新的索引位置,以便在发现重复字符时更新滑动窗口的起始位置。max_length记录最长子串的长度。最终,返回最长子串的长度。这个算法的时间复杂度是 O(n),其中 n 是字符串的长度。DEMO:
class Solution: def lengthOfLongestSubstring(self, s: str) -> int: char_index_map = {} # 用于记录字符的最新索引位置 max_length = 0 # 记录最长子串的长度 start = 0 # 滑动窗口的起始位置 for end in range(len(s)): if s[end] in char_index_map and char_index_map[s[end]] >= start: # 如果字符已经在窗口内,更新窗口的起始位置 start = char_index_map[s[end]] + 1 # 更新字符的最新索引位置 char_index_map[s[end]] = end # 更新最长子串的长度 max_length = max(max_length, end - start + 1) return max_length -
寻找两个正序数组的中位数
给定两个大小分别为
m和n的正序(从小到大)数组nums1和nums2。请你找出并返回这两个正序数组的 中位数 。算法的时间复杂度应该为O(log (m+n))。示例 1:
输入:nums1 = [1,3], nums2 = [2] 输出:2.00000 解释:合并数组 = [1,2,3] ,中位数 2示例 2:
输入:nums1 = [1,2], nums2 = [3,4] 输出:2.50000 解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5提示:
nums1.length == mnums2.length == n0 <= m <= 10000 <= n <= 10001 <= m + n <= 2000-106 <= nums1[i], nums2[i] <= 106
解题思路:
由于要求算法的时间复杂度为 O(log(m+n)),这提示我们可以考虑使用二分查找的思想。
首先,我们可以通过二分查找在较短的数组中选择一个分割点,然后根据这个分割点在另一个数组中找到对应的位置。如果两个分割点的值相等,说明我们找到了中位数。
DEMO:
def findMedianSortedArrays(nums1, nums2): if len(nums1) > len(nums2): nums1, nums2 = nums2, nums1 x, y = len(nums1), len(nums2) low, high = 0, x while low <= high: partitionX = (low + high) // 2 partitionY = (x + y + 1) // 2 - partitionX maxX = float('-inf') if partitionX == 0 else nums1[partitionX - 1] minX = float('inf') if partitionX == x else nums1[partitionX] maxY = float('-inf') if partitionY == 0 else nums2[partitionY - 1] minY = float('inf') if partitionY == y else nums2[partitionY] if maxX <= minY and maxY <= minX: if (x + y) % 2 == 0: return (max(maxX, maxY) + min(minX, minY)) / 2 else: return max(maxX, maxY) elif maxX > minY: high = partitionX - 1 else: low = partitionX + 1